全向轮运动学

本文简要介绍了全向轮的运动分解和模型公式推演。

全向轮

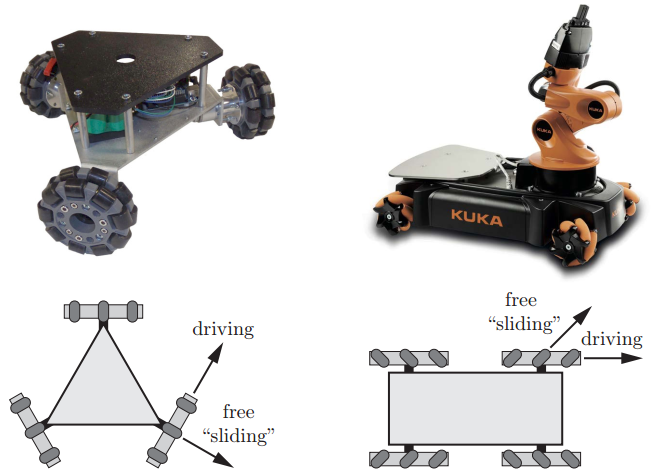
轮式移动机器人可分为两大类：全向和非全向的。全方位轮式移动机器人通常采用omniwheel或mecanum轮子。Omniwheels和Mecanum的轮子不是被操纵的，而是被向前或向后驱动的。由于他们的小直径滚轮，omniwheels和mecanum轮在坚硬的，平坦的地面表现得最好。

全方位运动系统中，Mecanum轮应用最广泛。Mecanum轮(又称瑞典轮)是瑞典Mecanum AB公司工程师Bengt Ilron提出的特殊轮系，其特点为沿轮毅圆周排布着与轮子成一定角度且可绕自身轴线进行旋转的辊子。由三个或以上Mecanum 轮按照一定方式排列组成的移动平台具有平面内三个自由度，可同时独立的前后、左右和原地旋转运动，可在不改变自身姿态的情况下向任意方向移动。

全向轮运动学

如下图所示，坐标系${S}$为空间中静止的参考系，坐标系${b}$固定在车身上随机器人运动。于是机器人的位置和姿态可以用向量$\vec{q}$来描述： $\vec{q}=(\phi,x,y)$ 在机体坐标系${b}$中的线速度及角速度为： $\vec{v_b}=(\omega_{bz},v_{bx},v_{by})$

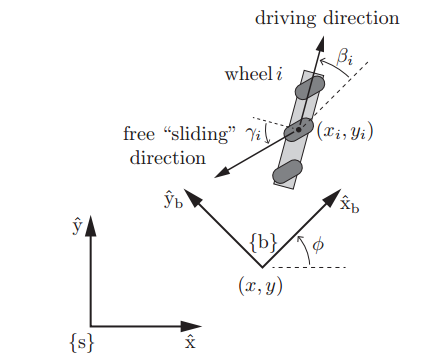
于是两坐标系下速度转换公式如下： $\begin{aligned} \vec{v_b}&=\left[ \begin{matrix} \omega_{bz}\\v_{bx}\\v_{by} \end{matrix} \right]&= \left[ \begin{matrix} 1&0&0\\ 0&\cos\phi&\sin\phi\\ 0&-\sin\phi&\cos\phi \end{matrix} \right] \left[ \begin{matrix} \dot{\phi}\\ \dot{x}\\ \dot{y} \end{matrix} \right]\tag{1}$ $\dot{q}&= \left[ \begin{matrix} \dot{\phi}\\ \dot{x}\\ \dot{y} \end{matrix} \right]&= \left[ \begin{matrix} 1&0&0\\ 0&\cos\phi&-\sin\phi\\ 0&\sin\phi&\cos\phi \end{matrix} \right] \left[ \begin{matrix} \omega_{bz}\\v_{bx}\\v_{by} \end{matrix} \right] \end{aligned}\tag{1}$

轮子的姿态在机体坐标系中的位置和子态可以表示为： $\vec{w} = (\beta_i,x_i,y_i)$

全向轮移动机器人必须安装至少三个，才能实现以任意三维速度$\dot{q}=(\dot{\phi},\dot{x},\dot{y})$进行移动。

为了控制全向移动机器人，我们需要知道给每个轮子多大的角速度才能使机器人达到目标速度$\dot{q}$。为了解答这个问题，我们需要理解单个轮子的运动学，为此建立如下图所示的轮子坐标系：

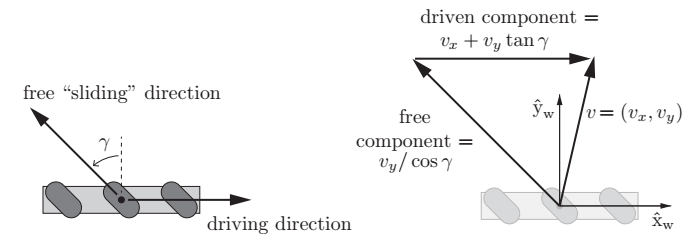
轮子坐标系$\hat{X_w}-\hat{Y_w}$建立在轮子中心，根据速度合成定理，车轮中心的速度$\vec{v}=(v_x,v_y)$满足下列公式： $\left[ \begin{matrix} v_x\\v_y \end{matrix} \right]= v_{drive} \left[ \begin{matrix} 1\\0 \end{matrix} \right]+ v_{slide} \left[ \begin{matrix} -\sin\gamma\\\cos\gamma \end{matrix} \right]\tag{2}$

其中$\gamma$为小辊子滚动方向与驱动轮平面的夹角（通常全向轮为0°，麦克纳姆轮为±45°），$v_{drive}$是沿轮子转动驱动速度，$v_{slide}$是沿辊子方向自由滑动的速度。

解$(2)$得到： $\begin{aligned} v_{drive} = v_x+v_y\tan\gamma\\ v_{slide} = \frac{v_y}{\cos\gamma} \end{aligned}$

设轮子半径为$r$，轮子转动角速度为$u$，根据上式得到： $\begin{aligned} u &= \frac{v_{drive}}{r}=\frac{v_x+v_y\tan\gamma}{r}\\ &=\frac{1}{r}\left[ \begin{matrix} 1&\tan\gamma \end{matrix} \right]\left[ \begin{matrix} v_x\\v_y \end{matrix} \right] \end{aligned}\tag{3}$

为了推导小车速度$\dot{q}=(\dot{\phi},\dot{x},\dot{y})$与轮子$i$角速度$u_i$之间的关系，联立上述方程： $\begin{aligned} u_i&=h_i(\phi)\dot{q}\\ &=\frac{1}{r_i}\left[ \begin{matrix} 1&\tan\gamma_i \end{matrix} \right] \left[ \begin{matrix} cos\beta_i&\sin\beta_i\\ -\sin\beta_i&\cos\beta_i \end{matrix} \right] \left[ \begin{matrix} -y_i&1&0\\x_i&0&1 \end{matrix} \right] \left[ \begin{matrix} 1&0&0\\ 0&\cos\phi&\sin\phi\\ 0&-\sin\phi&\cos\phi \end{matrix} \right] \left[ \begin{matrix} \dot{\phi}\\ \dot{x}\\ \dot{y} \end{matrix} \right] \end{aligned}$

从右到左进行解读：第一个变换矩阵将静止坐标系下的$\dot{q}$变换为小车局部坐标系${b}$中的$\vec{v}_b$；第二个变换矩阵将小车的局部速度转换为坐标系${b}$中的轮子线速度；第三个变换矩阵将坐标系${b}$中的轮子线速度转换为轮子坐标系$\hat{X_w}-\hat{Y_w}$中的线速度；最后一个变换矩阵将依据公式$(3)$计算轮子角速度。

合并矩阵，得到对轮子$i$的变换矩阵$h_i(\phi)$： $h_i(\phi)=\frac{1}{r_i\cos\gamma_i} \left[ \begin{matrix} x_i \sin (\beta +\gamma )-y_i \cos (\beta +\gamma )\\ \cos (\beta +\gamma +\phi )\\ \sin (\beta +\gamma +\phi )\\ \end{matrix} \right]^T\tag{4}$

对一个全向移动的机器人来说，当轮子数量$m\ge 3$时，矩阵$H(\phi)\in \R^{m\times 3}$。为了将参考系中的机器人速度$\dot{q}\in\R^3$转换为驱动轮子的角速度$\vec{u}\in\R^m$，将$m$行的$h_i(\phi)$向量组成矩阵$H(\phi)$，成为雅可比矩阵： $\vec{u} = H(\phi)\dot{q}= \left[ \begin{matrix} h_1(\phi)\\ h_2(\phi)\\ \vdots\\ h_m(\phi) \end{matrix} \right] \left[ \begin{matrix} \dot{\phi}\\ \dot{x}\\ \dot{y} \end{matrix} \right]\tag{5}$

同样可以计算机体坐标系下的速度和驱动轮子的角速度之间的关系，这其实就是$\phi=0$的一种特殊情况： $u=H(0)\vec{v}_b= \left[ \begin{matrix} h_1(0)\\ h_2(0)\\ \vdots\\ h_m(0) \end{matrix} \right] \left[ \begin{matrix} \omega_{bz}\\v_{bx}\\v_{by} \end{matrix} \right]\tag{6}$

车轮的位置和朝向$(\beta_i,x_i,y_i)$，以及辊子夹角$\gamma_i$的选择必须使得矩阵$H(0)$的秩为$3$。如果$rank(H) < 3$，则系统中存在奇异位形(singular configuration)，反映在运动学上就是失去部分自由度，即小车不能实现全方位运动。

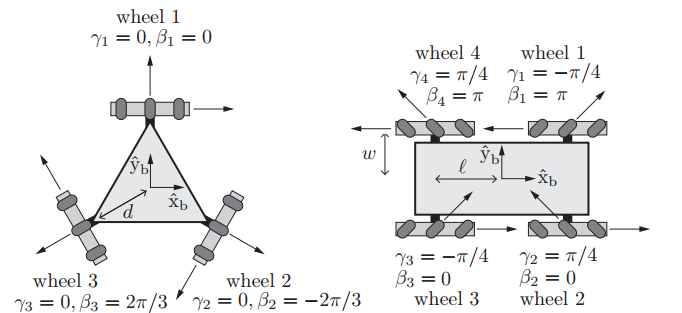
根据上面的公式，3个Omniwheel布置的移动机器人运动学模型为：

\[\vec{u} = \left[ \begin{matrix} u_1\\u_2\\u_3 \end{matrix} \right]=H(0)\vec{v}_b=\frac{1}{r} \left[ \begin{matrix} -d&1&0\\ -d&-\frac12&-\sin\frac{\pi}{3}\\ -d&-\frac12&\sin\frac{\pi}{3} \end{matrix} \right] \left[ \begin{matrix} \omega_{bz}\\v_{bx}\\v_{by} \end{matrix} \right]\tag{7}\]

4个Mecanum布置的移动机器人运动学模型为： $\vec{u}= \left[ \begin{matrix} u_1\\u_2\\u_3\\u_4 \end{matrix} \right]=H(0)\vec{v}_b=\frac{1}{r} \left[ \begin{matrix} l+w&-1&+1\\ l+w&+1&+1\\ l+w&+1&-1\\ l+w&-1&-1 \end{matrix} \right] \left[ \begin{matrix} \omega_{bz}\\v_{bx}\\v_{by} \end{matrix} \right]\tag{8}$

参考文献

Bae J J , Kang N . Design Optimization of a Mecanum Wheel to Reduce Vertical Vibrations by the Consideration of Equivalent Stiffness[J]. Shock and Vibration,2016,(2016-3-10), 2016, 2016(pt.4):1-8. 刘洲, 吴洪涛. Mecanum四轮全方位移动机构运动分析与仿真[J]. 机械设计与制造工程, 2011. 金磊, 秦训鹏, 华林,等. 辊子形状对Mecanum轮振动特性影响研究[J]. 机械传动, 2017, 041(006):67-74. Li Y , Dai S , Zhao L , et al. Topological Design Methods for Mecanum Wheel Configurations of an Omnidirectional Mobile Robot[J]. Symmetry, 2019, 11(10):1268-.