基于陀螺仪和双全向从动轮的坐标定位系统

　　在机器人的系统中，实时获取机器人当前位于场地的精确坐标显得尤为重要，并以此控制机器人的运动。本文旨在讲解基于陀螺仪和双全向从动轮的快速精确坐标定位系统。

机械模型

　　首先，建立机械模型，如图1所示，图中的两个轮子均为全向轮。为了方便模块化，使用了一体化结构设计。两个全向轮正交装配，全向轮的轮轴连接着编码器，并用直线轴承结合压簧，使全向轮时刻贴紧地面，减少打滑或悬空情况的发生。

图1 双全向轮模块机械设计图

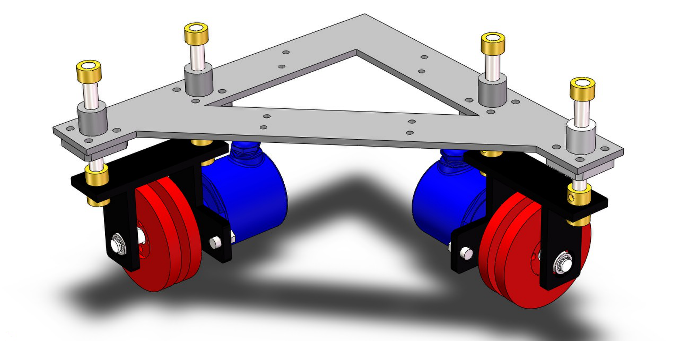
　　其次，对定位模型建模。从动轮坐标系S的原点在地面坐标系E中的坐标为( $x_{0}$ ,$y_0$)，夹角为A（逆时针为正），如下图所示。其中X，Y从动轮分别记录S坐标系中的x轴和y轴方向的位移。

图2 初始状态坐标关系

　　先分析简单的情况。假设机器人运动过程中偏航角不变，只进行平移运动。则由S坐标系到E坐标系的变换矩阵，可由公式(1)所表示，其中A表示S坐标系相对与E坐标系的夹角（逆时针为正）。

$R=\begin{bmatrix} cosA & -sinA\\ sinA & cosA \end{bmatrix} (1)$

　　假设已知t时刻的机器人坐标为( x_t , y_t )，并且在t时刻之后的∆t时间内，机器人只进行直线平移运动，可以得到公式(2)所示的t+∆t时刻的机器人坐标计算公式。其中，x_s和y_s分别表示在∆t时间内，X从动轮的位移记录和Y从动轮的位移记录。

$\begin{bmatrix} x_{t+\bigtriangleup t} & y_{t+\bigtriangleup t} \end{bmatrix}^{T} = \begin{bmatrix} x_{t} & y_{t} \end{bmatrix}^{T} + R\begin{bmatrix} x_{s} & y_{s} \end{bmatrix}^{T} (2)$

　　再分析复杂的情况，如机器人不仅进行平移运动，还混有各种复杂的弧线运动。假设从动轮坐标系在t时刻与地面坐标系的夹角为A_t，t+∆t时刻与地面坐标系的夹角为A_t+∆t。因机器人的运动一般较为平滑，偏航角不会突变，所以当∆t极小时，可以认为A_t+∆t与A_t近似相等。因此，在极短的时间∆t内，可以把这段运动等效为平移运动，只需将公式(1)中A进行重新定义，即可得到机器人坐标的关于时间的递推公式，如公式(3)-公式(5)所示。其中，x_s和y_s分别表示在∆t内，X从动轮的位移记录和Y从动轮的位移记录。

$A^{'}=\frac{A_{t}+A_{t+\bigtriangleup t}}{2} (3)$

$R_{t+\bigtriangleup t}=\begin{bmatrix} cosA^{'} & -sinA^{'}\\ sinA^{'} & cosA^{'} \end{bmatrix} (4)$

$\begin{bmatrix} x_{t+\bigtriangleup t} & y_{t+\bigtriangleup t} \end{bmatrix}^{T} = \begin{bmatrix} x_{t} & y_{t} \end{bmatrix}^{T} + R_{t+\bigtriangleup t}\begin{bmatrix} x_{s} & y_{s} \end{bmatrix}^{T} (5)$

　　需要注意的是，这里得到的是递推公式。利用这些公式，可以由前一时刻的坐标和从动轮陀螺仪的记录，计算出当前时刻的坐标。所以，在已知机器人初始坐标的情况下，可以利用上述公式不断迭代，快速地计算出当前坐标。这个模型的精确度依赖于迭代间隔∆t，∆t越小，模型的精确度越高。下一节将进行具体的误差分析。

误差分析和模型改进

　　上一节中，已将模型基本建好，现在来分析这个模型的误差，并进行优化和补偿。

　　首先是传感器的自身误差，这也是所有惯性定位方法中不可忽视的。在本文提出的定位模型中，主要体现在单轴陀螺仪的误差，它影响机器人的偏航角测量。由公式(3)-公式(5)可以看出，偏航角对模型的精度影响很大。对此的解决办法可以使用高精度单轴陀螺仪，如光纤陀螺仪等。也可以使用各种数字滤波方法，如卡尔曼滤波等。还可以辅以外界参考来进行偏航角数据融合，如电子罗盘等。

　　其次是模型的计算误差。建立这个模型的思想是一种微元的思想，因此，模型的精确度主要依赖于迭代的时间间隔∆t。所以在传感器采样周期允许的范围内，应该尽量缩短∆t。另外，这个模型主要是将弧线近似为直线，所以也可以尽量减少弧线运动，由此让定位更加精确。

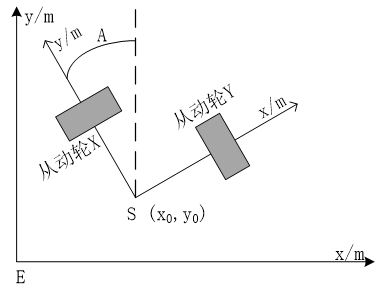
　　最后是从动轮的测量误差。虽说使用全向从动轮可以避免积分误差，得到精确的位移测量，但从动轮依靠地面来进行位移测量，这对地面的平整度要求较高。另外，当机器人进行自旋运动时，真实坐标变化不大。如果使用图3左边的安装方式，在机器人进行自旋运动时，从动轮也会跟着转动，模型会认为坐标改变，会造成较大的累计误差。

图3 从动轮的两种安装方式

　　相对于传感器误差和模型计算误差来说，从动轮造成的误差更大，也更需要解决。所以，下面主要阐述对地面不平整和旋转冗余量进行补偿和优化方法。

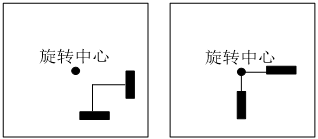
　　对于旋转冗余量问题，一个很自然的解决办法，就是从机械模型入手。让两个从动轮的轮毂延长线交于运动模型的旋转中心，如图3右边的安装方式所示。这样，机器人自旋时，两个从动轮都不会有记录值。但它加大了机械的设计和装配难度，也增大模块化的难度。所以，使用软件方式补偿是一种更好的选择。可以先记录下机器人自转时，两个从动轮分别记录的位移，以此得到一个旋转角度与旋转冗余量的线性关系。这样，可以在每次坐标计算前，把旋转冗余量去掉。

　　地面不平整的问题，这也是一个关键的问题。从动轮必须时刻贴紧地面，否则会悬空或打滑。而地面多少会凹凸不平，这就造成从动轮记录的位移实际上比真实的位移要大。举个例子，如果从动轮经过横截面如图4左边所示的地面，被记录的量是弧线S的长度，而不是直线L的长度。

图4 地面不平整示意图

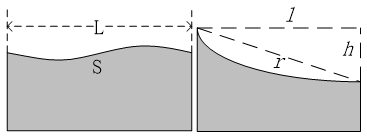
　　这里依然可以用微元法思想，对地面不平整进行补偿。假定地面的凹凸程度是较为连续的，不会出现很大的断层。在较短的时间内，可以将从动轮经过的弧线轨迹近似为直线，如图4右边所示的r直线。需要得到的量为真实水平位移，也就是图4右边所示的l直线的长度。而l与r、h构成直角三角形，当已知r和h，即可求出l。r可以用从动轮的位移测量值来近似。h为两次距离记录之间的高度差，可以使用直线位移传感器配合数模转换模块来得到。