基于梯度下降法的姿态航向参考系统

　　本文介绍了基于梯度下降法的姿态航向参考系统。

符号，术语和约定

　　先对姿态航向参考系统进行建模。为了建模方便，在建模前，我们先进行如下的约定。

　　所有坐标系均使用右手坐标系^[15]。

　　使用地球为绝对坐标系，使用E表示，以“天”为$Z$轴，“东”为$X$轴，“北”为$Y$轴。

　　传感器坐标系如图4-1所示，使用$S$表示。

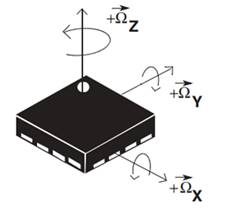
　　三轴陀螺仪获取的三个轴向的数据分别用$W_x$，$W_y$，$W_z$，分别代表$X$轴，$Y$轴，$Z$轴的角速度，单位使用弧度/秒。

　　三轴加速度计获取的三个轴向的数据分别用$a_x$，$a_y$，$a_z$，分别代表$X$轴，$Y$轴，$Z$轴的加速度。

　　三轴磁力计获取的三个轴向的数据分别用$m_x$，$m_y$，$m_z$，分别代表$X$轴，$Y$轴，$Z$轴的磁场。

　　为便于描述，没特殊说明的话，下文均把${}_{E}^{S}q$，默认简写成$Q$,表示传感器坐标系相对于地球坐标系的姿态对应的四元数。

由三轴陀螺仪获取姿态

　　我们首先考虑最简单的情况，只用三轴陀螺仪来获取姿态。

　　我们定义一个S中的四元数向量${}^{S}W$，用于表示角速度，如公式 $\ref{4-1}$ 所示。根据文献^[11]，四元数$\hat{Q}$的导数$\dot{Q}$可由公式 $\ref{4-2}$ 计算得到，它表示姿态变化的速率。

\begin{equation} \label{4-1} ^S W=\begin{bmatrix} 0 & W_x & W_y & W_z \end{bmatrix} \end{equation}

\begin{equation} \label{4-2} \dot{Q}=\frac{1}{2}\hat{Q}\ \otimes \,{}^{S}W \end{equation}

　　我们用$Q_{W,t}$来表示在t时刻，传感器坐标系相对于与地球坐标系的姿态。如果初始状态已知的话，则$Q_{W,t}$可由四元数的导数$\dot{Q}_{W,t}$积分得到，如公式 $\ref{4-3}$ 和公式 $\ref{4-4}$ 所示。其中$\hat{Q}_{est,t-1}$表示$t-1$时刻的姿态估计值，${}^{S}W_{t}$为$t$时刻的陀螺仪测量值，$\Delta t$为采样时间间隔，下标w表示这个四元数是由角速度得到的。

\begin{equation} \label{4-3} \dot{Q}_{W,t}=\frac{1}{2}\hat{Q}_{est,t-1}\ \otimes {}^{S}W_{t} \end{equation}

\begin{equation} \label{4-4} Q_{W,t}=\hat{Q}_{est,t-1}+{\dot{Q}}_{W,t}\Delta t \end{equation}

　　于是，我们可根据公式 $\ref{4-4}$ 得到由陀螺仪获取的姿态。

由“场”获取姿态

　　一个三轴加速度计可以测量重力场的大小和方向，同时会因为传感器运动时产生的线性加速度而受到影响。相似的，三轴磁力计也可测量磁场的方向和大小，但也会被近场磁场干扰。在本文建立的模型中，为了理想建模，忽略这些干扰，即假定加速度计只测量重力，磁力计只测量地磁场。

　　如果场的方向在地球坐标系中已知，根据传感器坐标系中测量到的场的方向，则可以计算出传感器坐标系相对于地球坐标系的姿态。然而，对于任意的测量值，这个姿态解并不是唯一的，因为真实的姿态绕着场的方向旋转得到的姿态的测量值都是一样的。而四元数要求的姿态必须是一个完整的姿态，而通过场得到的姿态是不完全的。这就需要我们去找到一个最优的姿态解，使其与真实的姿态解误差最小。

　　这就可以当成一个最优化问题来求解，我们定义最优解的误差函数，如公式 $\ref{4-6}$ 所示，当满足公式 $\ref{4-5}$ 时，理论上$\hat{Q}$可找到一个最优解，使得姿态的误差最小。其中，${}^{E}\hat{d}$表示场在地球坐标系中的方向向量，${}^{S}\hat{s}$表示传感器坐标系中的场方向的测量值。

\begin{equation} \label{4-5} \underset{\hat{Q}\in {R}^4}{\mathop{\min }}\,f(\hat{Q},{}^{E}\hat{d},{}^{S}\hat{s}) \end{equation}

\begin{equation} \label{4-6} f(\hat{Q},{}^{E}\hat{d},{}^{S}\hat{s})\ =\,{\hat{Q}^{*}}\ \otimes \,{}^{E}\hat{d}\,\otimes \,\hat{Q}\,\,-\,{}^{S}\hat{s} \end{equation}

\begin{equation} \label{4-7} \hat{Q}=\left[ {q}_{1}\ {q}_{2}\ {q}_{3}\ {q}_{4} \right] \end{equation}

\begin{equation} \label{4-8} {}^{E}\hat{d}=\left[ 0\ {d}_{x}\ {d}_{y}\ {d}_{z} \right] \end{equation}

\begin{equation} \label{4-9} {}^{S}\hat{s}=\left[ 0\ {s}_{x}\ {s}_{y}\ {s}_{z} \right] \end{equation}

　　最优化算法有很多种，其中梯度下降法是一种简单高效的算法，公式 $\ref{4-10}$ 描述了梯度下降法如何用第$k$次迭代的结果来估计第$k+1$次的值^[7]。其中，$u$为迭代的步长，初始状态${\hat{Q}_{0}}$已知。$\nabla f(\hat{Q},{}^{E}\hat{d},{}^{S}\hat{s})$为公式 $\ref{4-5}$ 定义的误差函数的解曲面的梯度，它可由误差函数和误差函数的Jacobian 矩阵计算得到，如公式 $\ref{4-11}$ 所示^[16]。根据公式 $\ref{4-6}$ ，可得公式 $\ref{4-12}$ ，为了方便计算，转换成3维向量。误差函数的Jacobian 矩阵可由公式 $\ref{4-13}$ 计算得到。

\begin{equation} \label{4-10} {Q}_{k+1}={\hat{Q}_k}-u\frac{\nabla f({\hat{Q}_k},{}^{E}\hat{d},{}^{S}\hat{s})\ }{\left| \nabla f({\hat{Q}_k},{}^{E}\hat{d},{}^{S}\hat{s}) \right|\ },k=0,1,2…n \end{equation}

\begin{equation} \label{4-11} \nabla f({\hat{Q}_k},{}^{E}\hat{d},{}^{S}\hat{s})={J}^{T}({\hat{Q}_k},{}^{E}\hat{d})f({\hat{Q}_k},{}^{E}\hat{d},{}^{S}\hat{s}) \end{equation}

\begin{equation} \label{4-12} f({\hat{Q}_k},{}^{E}\hat{d},{}^{S}\hat{s})= \begin{bmatrix} 2d_x(\frac{1}{2}-q_3^2-q_4^2)+2d_y(q_1 q_4+q_2 q_3)+2d_z(q_2 q_4-q_1 q_3)-s_x\\2d_x(q_2 q_3-q_1 q_4)+2d_y(\frac{1}{2}-q_2^2-q_4^2)+2d_z(q_1 q_2+q_3 q_4)-s_y\\2d_x(q_1 q_3+q_2 q_4)+2d_y(q_3 q_4-q_1 q_2)+2d_z(\frac{1}{2}-q_2^2-q_3^2)-s_z\end{bmatrix} \end{equation}

\begin{equation} \label{4-13} J({\hat{Q}_k},{}^{E}\hat{d})= \begin{bmatrix}2{d_y}{q_4}-2{d_z}{q_3} & 2{d_y}{q_3}+2{d_z}{q_4} & -4{d_x}{q_3}+2{d_y}{q_2}-2{d_z}{q_1} & -4{d_x}{q_4}+2{d_y}{q_1}+2{d_z}{q_2}\\-2{d_x}{q_4}+2{d_z}{q_2} & 2{d_x}{q_3}-4{d_y}{q_1}+2{d_z}{q_1} & 2{d_x}{q_2}+2{d_z}{q_4} & -2{d_x}{q_1}-4{d_y}{q_4}+2{d_z}{q_3}\\2{d_x}{q_3}-2{d_y}{q_2} & 2{d_x}{q_4}-2{d_y}{q_1}-4{d_z}{q_2} & 2{d_x}{q_1}+2{d_y}{q_4}-4{d_z}{q_3} & 2{d_x}{q_2}+2{d_y}{q_3}\end{bmatrix} \end{equation}

　　接着，我们可以把上述公式套入重力场中，如公式 $\ref{4-14}$ ， $\ref{4-15}$ ， $\ref{4-16}$ ， $\ref{4-17}$ 所示。一般来说，我们可以假定重力场方向为地球坐标系的$Z$轴方向。

\begin{equation} \label{4-14} {}^{E}\hat{g}=\left[ 0\ 0\ 0\ 1 \right] \end{equation}

\begin{equation} \label{4-15} {}^{S}\hat{a}=\left[ 0\ {a_x}\ {a_y}\ {a_z} \right] \end{equation}

\begin{equation} \label{4-16} {f_g}(\hat{Q},{}^{E}\hat{g},{}^{S}\hat{a})= \begin{bmatrix}2({q_2}{q_4}-{q_1}{q_3})-{s_x}\\2({q_1}{q_2}+{q_3}{q_4})-{s_y}\\2(\frac{1}{2}-{q_2}^{2}-{q_3}^{2})-{s_z}\end{bmatrix} \end{equation}

\begin{equation} \label{4-17} {J_g}(\hat{Q},{}^{E}\hat{g})=\begin{bmatrix}-2{q_3} & 2{q_4} & -2{q_1} & 2{q_2}\\2{q_2} & 2{q_1} & 2{q_4} & 2{q_3}\\0 & -4{q_2} & -4{q_3} & 0 \end{bmatrix} \end{equation}

　　相似的，我们可以把这些公式代入地磁场。如公式 $\ref{4-18}$ ， $\ref{4-19}$ ， $\ref{4-20}$ ， $\ref{4-21}$ 所示。需要注意的是，磁场的方向并不像重力场那么确定，会随着地理位置而改变，如北京和伦敦的地磁场是不一样的^[17]。所以我们将磁场方向分解为水平方向和垂直方向，如公式 $\ref{4-19}$ 所示。

\begin{equation} \label{4-18} {}^{E}\hat{b}=\left[ 0\ {b_x}\ 0\ {b_z} \right] \end{equation}

\begin{equation} \label{4-19} {}^{S}\hat{m}=\left[ 0\ {m_x}\ {m_y}\ {m_z} \right] \end{equation}

\begin{equation} \label{4-20} {f_b}(\hat{Q},{}^{E}\hat{b},{}^{S}\hat{m})= \begin{bmatrix}2{b_x}(\frac{1}{2}-{q_3}^{2}-{q_4}^{2})+2{b_z}({q_2}{q_4}-{q_1}{q_3})-{m_x}\\2{b_x}({q_2}{q_3}-{q_1}{q_4})+2{b_z}({q_1}{q_2}+{q_3}{q_4})-{m_y}\\2{b_x}({q_1}{q_3}+{q_2}{q_4})+2{b_z}(\frac{1}{2}-{q_2}^{2}-{q_3}^{2})-{m_z}\end{bmatrix} \end{equation}

\begin{equation} \label{4-21} {J_b}(\hat{Q},{}^{E}\hat{b})=\begin{bmatrix}-2{b_z}{q_3} & 2{b_z}{q_4} & -4{b_x}{q_3}-2{b_z}{q_1} & -4{b_x}{q_4}+2{b_z}{q_2}\\-2{b_x}{q_4}+2{b_z}{q_2} & 2{b_x}{q_3}+2{b_z}{q_1} & 2{b_x}{q_2}+2{b_z}{q_4} & -2{b_x}{q_1}+2{b_z}{q_3}\\2{b_x}{q_3} & 2{b_x}{q_4}-4{b_z}{q_2} & 2{b_x}{q_1}-4{b_z}{q_3} & 2{b_x}{q_2}\end{bmatrix} \end{equation}

　　如上文提到的，单独使用重力场或者地磁场来获取姿态的话，姿态解不是唯一的。所以，我们可以将重力场和地磁场的解组合到一起，如公式 $\ref{4-22}$ 和公式 $\ref{4-23}$ 所示。

\begin{equation} \label{4-22} {f_{g,b}}(\hat{Q},{}^{E}\hat{g},{}^{S}\hat{a},{}^{E}\hat{b},{}^{S}\hat{m})=\begin{bmatrix}{f_g}(\hat{Q},{}^{E}\hat{g},{}^{S}\hat{a})\\{f_b}(\hat{Q},{}^{E}\hat{b},{}^{S}\hat{m})\end{bmatrix} \end{equation}

\begin{equation} \label{4-23} {J_{g,b}}(\hat{Q},{}^{E}\hat{g},{}^{E}\hat{b})=\begin{bmatrix}{J_g}(\hat{Q},{}^{E}\hat{g})\\{J_b}(\hat{Q},{}^{E}\hat{b})\end{bmatrix} \end{equation}

　　根据公式 $\ref{4-10}$ ，我们可以得到姿态的梯度下降法递推公式，如公式 $\ref{4-24}$ 所示。其中${\hat{Q}_{est,t-1}}$为$t-1$时刻的姿态估计值。$u_t$为梯度下降的步长。至此，我们可以得到使用梯度下降法求解由重力场和地磁场获得姿态的算法。

\begin{equation} \label{4-24} Q_{\nabla ,t}={\hat{Q}_{est,t-1}}-{u_t}\frac{\nabla f}{\parallel \nabla f \parallel} \end{equation}

\begin{equation} \label{4-25} \nabla f={J_{g,b}}^{T}(\hat{Q},{}^{E}\hat{g},{}^{E}\hat{b}){f_{g,b}}(\hat{Q},{}^{E}\hat{g},{}^{S}\hat{a},{}^{E}\hat{b},{}^{S}\hat{m}) \end{equation}

传感器数据融合

　　上文中，已由公式 $\ref{4-4}$ 得到由陀螺仪求解姿态的算法， $\ref{4-24}$ 得到由加速度计，磁力计求解姿态的算法。现在我们将这两个姿态解融合，如公式 $\ref{4-26}$ 所示，其中${Q_{\nabla ,t}}$由公式 $\ref{4-14}$ 定义，${Q_{W ,t}}$由公式 $\ref{4-4}$ 定义，$r_t$和$(1-r_t)$分别为他们对应的权重。

\begin{equation} \label{4-26} {Q_{est,t}}={r_t}{Q_{\nabla ,t}}+(1-{r_t}){Q_{W,t}},0\le {r_t}\le 1 \end{equation}

　　接下来问题的关键就是确定$r_t$。由于公式 $\ref{4-4}$ ，可知${Q_{W ,t}}$的计算是一个不断积分的过程，所以${Q_{W ,t}}$是发散的。由公式 $\ref{4-24}$ ，可知${Q_{\nabla ,t}}$在不断的逼近极值，所以${Q_{\nabla ,t}}$是收敛的。为了得到一个稳定的姿态，我们应该让${Q_{\nabla ,t}}$收敛权重的和${Q_{W ,t}}$的发散权重相等^[7]。${Q_{\nabla ,t}}$的收敛率可由$\frac{u_t}{\Delta t}$来表示，用$\beta $来表示${Q_{W ,t}}$的发散率，也就是陀螺仪的测量误差。这样我们可以写出公式 $\ref{4-27}$ ，从而计算出出关于$r_t$的公式 $\ref{4-28}$ 。

\begin{equation} \label{4-27} (1-{r_t})\beta ={r_t}\frac{u_t}{\Delta t} \end{equation}

\begin{equation} \label{4-28} {r_t}=\frac{\beta }{\frac{u_t}{\Delta t}+\beta } \end{equation}

　　公式4-26可展开为：

\begin{equation} \label{4-29} {Q_{est,t}}=\frac{\beta }{\frac{u_t}{\Delta t}+\beta }({\hat{Q}_{est,t-1}}-{u_t}\frac{\nabla f}{\parallel \nabla f \parallel})+(1-\frac{\beta }{\frac{u_t}{\Delta t}+\beta })({\hat{Q}_{est,t-1}}+{\dot{Q}_{W,t}}\Delta t) \end{equation}

　　化简可得：

\begin{equation} \label{4-30} {Q_{est,t}}={\hat{Q}_{est,t-1}}+m({\dot{Q}_{W,t}}-\beta \frac{\nabla f}{\parallel \nabla f \parallel})\Delta t \end{equation}

\begin{equation} \label{4-31} m=\frac{u_t}{u_t+\beta \Delta t} \end{equation}

　　至此我们得到姿态航向参考系统的模型，如公式 $\ref{4-30}$ 所示，我们只需确定两个参数，步长$u_t$和陀螺仪测量误差$\beta$，即可实现这个模型。

模型参数确定

　　在上文中，我们已经将姿态航向参考系统进行建模，还差两个待确定参数。在这里将确定这两个参数的具体数值，并对模型的性能进一步优化。

　　为了方便计算，我们可做如下假设，假设采样时间足够短，且陀螺仪误差较小，则由公式 $\ref{4-31}$ 可认为$m\approx 1$。如此，便可消去步长$u_t$这个参数。

　　即可得到

\begin{equation} \label{5-1} {Q_{est,t}}={\hat{Q}_{est,t-1}}+({\dot{Q}_{W,t}}-\beta \frac{\nabla f}{\parallel \nabla f \parallel})\Delta t \end{equation}

　　现在公式已大幅简化，唯一不确定的就是$\beta$参数。

　　$\beta$指的是陀螺仪的测量误差，可以根据数据手册^[18]来获取，但本文打算使用实际测量的误差。根据公式 $\ref{4-2}$ ，可推导出公式 $\ref{5-2}$ ，其中，$d$为陀螺仪的静态飘移量，$q$为任意的单位四元数。因此，我们可以通过陀螺仪的数据手册来或直接对陀螺仪的数据采样分析计算得到$\beta$。

\begin{equation} \label{5-2} \beta =\parallel \frac{1}{2}q\otimes \left[ 0\ d\ d\ d \right] \parallel=\sqrt{\frac{3}{4}}d \end{equation}

　　至此，我们可以最终确定我们所需要的姿态航向参考系统模型了。

磁场干扰补偿

　　在建立好模型后，还有一个比较重要的问题要考虑，就是磁场干扰的问题。

　　地磁场很容易被近场磁场干扰，如电机，金属家具，金属。造成的磁场干扰，没有外部的方向参考的话，无法被校正。竖直方向的磁场，可由重力场校正，水平方向的磁场，则可利用GPS^[19]等进行校正。

　　在本文中，没有使用GPS等全球定位技术，因此，对于航向角，无法提供可以校正的外部参考。所以，本文提出的姿态航向参考系统，以上电时的状态作为初始航向角，之后的航向角都以初始姿态的角度作为基准，如公式 $\ref{5-3}$ ， $\ref{5-4}$ 所示。

\begin{equation} \label{5-3} {}^{E}\hat{h}=[0\ h_x\ h_y\ h_z]={\hat{Q}_{est,t-1}}\otimes {}^{S}{\hat{m}_{t}}\otimes \hat{Q}_{est,t-1}^{*} \end{equation}

\begin{equation} \label{5-4} {}^{E}{\hat{b}_t}=[0 \sqrt{h_x{}^{2}+{h_y}^{2}}\ 0\ {h_z}] \end{equation}

　　这样，当外界的磁场干扰较为稳定时，获得的偏航角也较为稳定。

性能优化

　　鉴于使用的处理器为嵌入式芯片，计算性能远没有桌面计算机强大，除了姿态航向参考系统，还有很多其他的任务要处理，所以系统应该要尽可能地降低计算负担。

　　相比欧拉角等其他姿态表示方法，四元数的计算负担很小，不需要使用任何三角函数，但依然存在可以优化的地方。本文主要从两个地方来进行优化。

　　1、四元数的规范化。

　　四元数的规范化，即让四元数的模长为1，上文的所有公式中，参与计算的四元数都是规范的四元数，所以在每一次迭代计算完成时，都应对四元数进行规范化，四元数的规范化公式如下：

\begin{equation} \label{5-5} \hat{q}=\frac{\text{q}}{\parallel q \parallel}=\frac{q}{\sqrt{q_1{}^{2}+{q_2}^{2}+{q_3}^{2}+{q_4}^2}} \end{equation}

　　四元数的规范化需要计算平方根的倒数，这是一笔不小的计算开销。根据文献^[20]提供的一种快速计算平方根的倒数的方法，也就是业界中传奇的“0x5f3759df”算法，始于一个3D游戏《雷神之锤3》。代码如下：

float invSqrt(float x)
{
    float halfx = 0.5f * x;
    float y = x;
    long i = *(long *)&y;
    i = 0x5f3759df - (i >> 1);
    y = *(float *)&i;
    y = y * (1.5f - (halfx * y * y));
    return y;
}

　　2、合并重复计算。

　　在公式 $\ref{4-16}$ ， $\ref{4-17}$ ， $\ref{4-20}$ ， $\ref{4-21}$ 中，有大量的重复计算，可采取以空间换时间的方法。